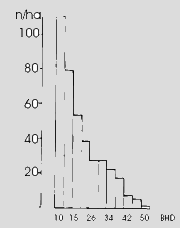Stammzahlverteilungen
Stammzahlverteilungskurven
In kleineren Beständen bzw. bei nur stichprobeweisen Aufnahmen in Beständen, ist die Verteilung der Stämme auf die BHD-Stufen mehr oder minder unregelmäßig. Da die Verteilung der Stämme auf die BHD-Klassen einerseits ein wichtiges Strukturmerkmal für die waldbauliche Beurteilung der Bestände ist und anderseits wertvolle Auskünfte über die
Sortenverteilung, die ihrerseits betriebswirtschaftlich bedeutungsvoll ist, gibt, bestehen verschiedene Überlegungen, wie die Stammzahlverteilungen ausgeglichen, d.h. durch theoretische Verteilungen beschrieben werden können.
Allgemein gilt, daß in dichten Beständen, in denen die natürliche Mortalität infolge der Konkurrenz schon eingetreten ist oder durch niederdurchforstungsartige Eingriffe die Stämme vom schwächeren Ende her genutzt wurden, die Stammzahlverteilung deutlich linksschief wird. Die unten stehende Abbildung zeigt die Stammzahlverteilung einer
Probefläche in einer Fichtendickung mit mehr als 100.000 Stämmen/ha.
5 Jahre später waren auf dieser Fläche nur mehr 72.000 Stämme/ha angetroffen worden. Die Mortalität (34 % der Stammzahl) trat überproportional am schwächsten Ende der Durchmesserverteilung ein. Durch das höhere Dickenwachstum der stärkeren Stämme (Zuwachsgerade mit positivem Anstieg) streckt sich die Verteilung nach
rechts und wird im Zusammenwirken von Mortalität und Zuwachs immer deutlicher linksschief.
Die nächste Abbildung zeigt eine Fichtenaufforstung mit 6000 Stämmen/ ha nach 20 Jahren. Die Mortalität war gering (5 %). Die ursprüngliche Verteilung beim Erreichen der Brusthöhe kann man sich als Gleichverteilung vorstellen. Vor dem Einsetzen der natürlichen konkurrenzbedingten Mortalität werden solche Verteilungen leicht rechtsschief.
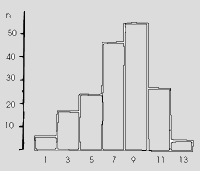
Mit zunehmendem Alter werden die Stammzahlverteilungen breiter, flacher und symmetrischer. Nach Auslesedurchforstungen werden die Stammzahlverteilungen kurzfristig zweigipfelig, später wieder symmetrisch.
Eine Ausnahme bilden die Stammzahlverteilungen in Plenterwäldern. Sie sind meist durch negative Exponentialverteilungen darstellbar.
Ähnlich wie bei der Höhenkurve scheint es sinnvoll, Stammzahlverteilungen aus der Kenntnis von Stichproben mittels theoretischer Verteilungsfunktionen auszugleichen. Es genügt dann die Kenntnis der entsprechenden Parameter (Mittelwerte, Standardabweichungen oder Perzentilen), um die Häufigkeiten in den BHD-Stufen berechnen zu können.
Die älteste diesbezügliche Verteilungsfunktion wird von SCHIFFEL und FEKETE für die Fichte beschrieben. Sie stellt den Durchmesser in Prozent des Durchmessers des Grundflächenmittelstammes als Funktion der prozentischen Summenhäufigkeit dar: Weitere, üblicherweise zur Darstellung von Stammzahlverteilungen verwendete, Verteilungsfunktionen sind:
- die gestutzte Normalverteilung
- die Log-Normalverteilung
- die Beta-Verteilung
- die Gamma-Verteilung
- die Weibull–Verteilung
Unser System verwendet zur Berechnung der Stammzahlverteilung eine sogenannte "Gamma - Verteilung". Weitere Informationen zur Gamma - Verteilung finden Sie hier.